Flow and Deliberate Practice are rather popular concepts these days. This shouldn’t be surprising, as everyone wants to be fulfilled in their work and play, and many people want to become an expert in some domain. However, proponents of each approach appear to be in conflict a lot of the time. On top of that, some people think they are the same thing! I believe that they are separate but compatible: two aspects of the same consistent model.
In an email thread among alumni of CFAR’s rationality workshops, one member commented with a few paragraphs to this effect:
What good SNS* looks like is being in a Flow state. A Flow state is a state in which you are intensely pushing yourself, to the limits of your abilities, toward a goal you are intrinsically motivated to pursue, and receiving frequent and immediate feedback on your progress.
*SNS: for a relevant discussion of the Sympathetic Nervous System, see my earlier post on Againstness Training from a few months ago.
I responded with
I do agree that good SNS looks like what’s described here. At the very least, anything that feels “intense” is almost certainly SNS, and this state you describe is clearly good.
However, I don’t believe this is flow. I think the term you’re looking for is deliberate practice. The turbocharging class/concept [taught by CFAR] is basically a framework for turning anything into deliberate practice.
A fascinating look into a very fundamental part of the psychology of happiness and life satisfaction.
What this exchange reveals, however, is the ambiguity in the word “flow”. When Mihaly Csikszentmihalyi did his original research, the state of balance people were finding during their work was overwhelmingly described by them as “flow”, implying that that is a good word to use for this experience of balance between skill and challenge. It appears, though, that there are false positives: experiences that are not what Csikszentmihalyi calls “flow” but which other people intuitively do. This, I believe, is a key source of the confusion around deliberate practice. The satisfying nature of it and the sense of growth evoke a feeling of flowing in some people.
And so both the canonical Flow, and Deliberate Practice are both sometimes referred to as “flow”.
Much as Csikszentmihalyi is the man behind Flow, there is a man behind Deliberate Practice: K Anders Ericsson, a professor at Florida State University, who has spent years studying how people become experts at something. If you’re thinking 10,000 hours, you’re right. Malcolm Gladwell popularized that idea but it has its origins in Ericsson’s research. What Ericsson discovered is that experts in a given domain have typically spent not just ten thousand hours practising relevant skills in that field, but that they’ve done that practice a certain way. Essentially it boils down to performing at a level slightly beyond what’s comfortable.
(Update 2020-04-07: It also requires adequate feedback loops, and may only apply to certain fields. I’m pretty skeptical of applying the 10,000 hours model to anything other than chess, concert violin, or competitive running/swimming. Basically only in cases where there’s only one thing it means to be an expert.)
One concept from Ericsson’s work that I’m familiar with was exposed to me via Moonwalking with Einstein, a book about memory (which I summarized on actionablebooks.com). Joshua Foer, the author of Moonwalking, called it the OK Plateau, and it occurs because your brain doesn’t want to have to strain. Your brain wants to do things unconsciously, so it tries to learn them so effectively that it doesn’t have to pay attention while you do them. This is great for performance or multitasking (talking while driving, for example) but totally halts learning and improvement, hence it will not get you to expertise.
In the book, Foer has hit a plateau on his times for speed cards (memorizing the order of an entire deck of cards). Ericsson, who is coaching him, recommends he sets a metronome and tries to go just 10-20% faster than his current ability, memorizing a card each time the metronome ticks. This single intervention starts Foer on the path to improvement again, and he goes on to set a U.S. record in speed cards in his first competition.
To help distinguish between flow and deliberate practice, consider this image, which I created based on an chart in Mihaly Csikszentmihalyi’s book Flow. Flow is described as the state that occurs when skill and challenge are perfectly balanced such that the act is neither straining nor boredom, and only occurs when you’re in the “flow channel” (white, in the diagram). Deliberate practice, on the other hand, requires challenging yourself beyond your current skill level, i.e. going into the Anxiety section (hence SNS). As this diagram illustrates (point #3) there’s a tension that occurs when that happens, forcing you to level up your skills. Obviously you don’t want to make it too challenging, or you’ll be unable to perform without mistakes, at which point you’re practising making mistakes.
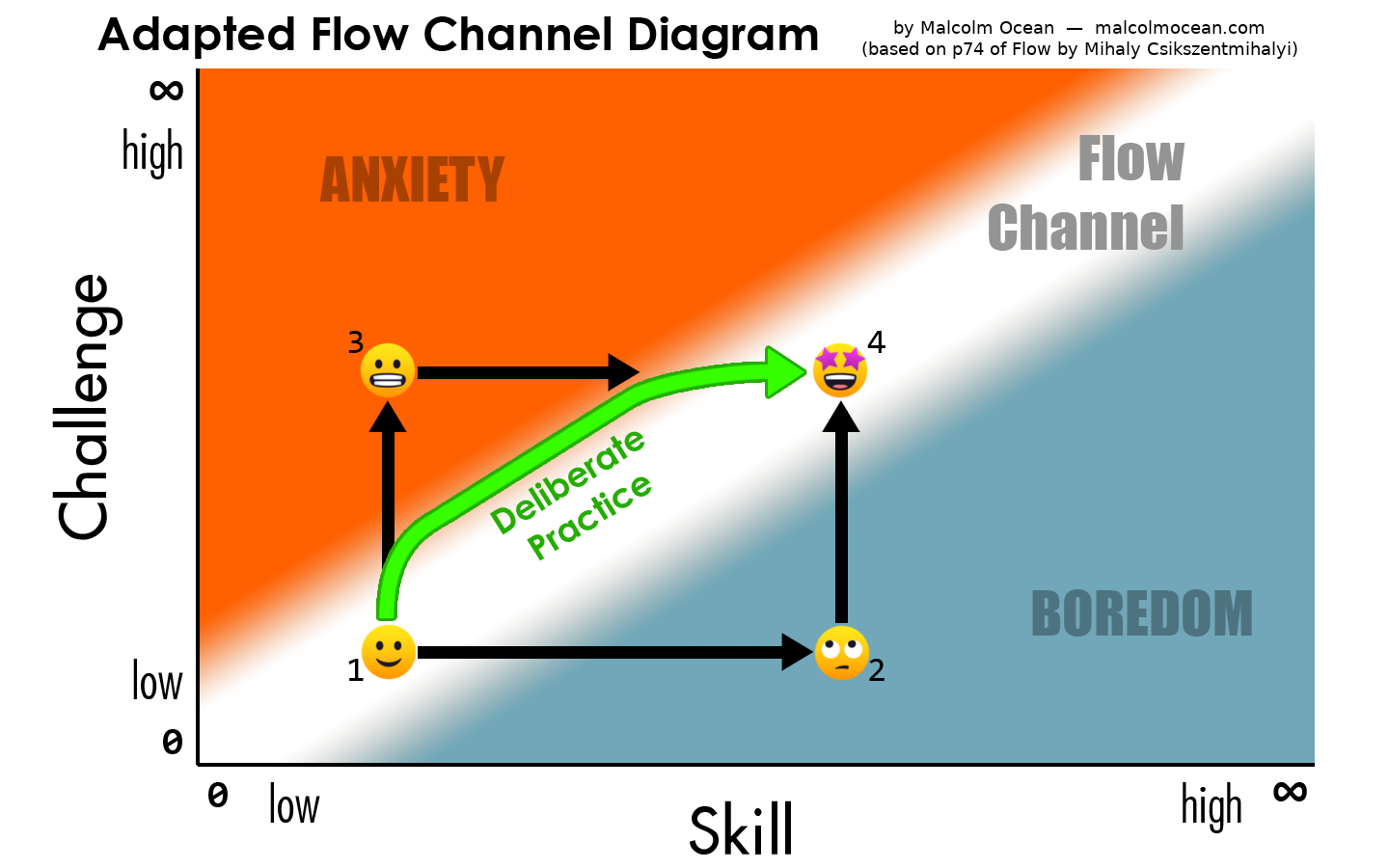
Image by Malcolm Ocean, based on an image in the original Flow book. License CC BY-SA
I read Flow a few months ago, and many of the examples he gives are clearly not deliberate practice / learning. In fact, they’re things like rural farmers who do their work with a deep sense of presence. Sure, they’re honing their craft, but it’s not the kind of rapid-skill building that turbo-charging / deliberate practice is. It seems self-evident to me that the Flow state at 4 is much more pleasurable than the flow state at 1. This is also supported by the following model from Csikszentmihalyi’s later book, Finding Flow (which I haven’t read; I retrieved the image from Wikipedia). This suggests that deliberate practice, in addition to making your performance more effective (and therefore more valuable, etc.) will also make your performance more enjoyable.
Deliberate practice is rare, because it’s hard work. People will naturally tend towards flow states, which are more enjoyable, but which make for substantially slower learning and growth. Essentially, you want to be performing in a flow state, but training using deliberate practice. Flow is when you’re playing all the way through a piece of music that’s exactly at your skill level; deliberate practice is going over bar 39 thirty-nine times to nail the complex rhythm. Ideally, you’ll probably do a bit of eat.
Flow periods may be necessary for maintaining motivation and big-picture perspective: chess masters may have spent the majority of their time reviewing grand master games, but they typically don’t give up playing games altogether during that time. The key is to find the balance that works best for you: balance between skill and challenge, and between flow and deliberate practice. The following maxim is a pretty good start though:
(Before, during, and essentially after writing this, I discovered several other relevant articles, listed below. They speak in some way to the same point I’m making, but I found I wanted an even more explicit relationship between the concepts. Also, in the interests of my own self-improvement and of making effective models of concepts, I would love to hear what you think about this article! Leave a comment letting me know if this makes sense, or if you think it could be improved.)
Constantly consciously expanding the boundaries of thoughtspace and actionspace. Creator of Intend, a system for improvisationally & creatively staying in touch with what's most important to you, and taking action towards it.
Becs » 21 Jun 2016 »
Oh, I am so interested in this question. I work in the field of sports coaching, specifically training skiers to be instructors.
My conflict is that deliberate practice has to be different from flow. I believe that DP is what will create and strengthen neural pathways meaning that ‘chunks’ can be stored in long term memory, ready to be accessible in flow state performance.
When training skiers, I find that we have people often present themselves for assessment who need to be working in deliberate practice mode to hone their skill in order to create the performance required to pass the test.
The organisation I work for aims to provide training and continual assessment which makes it pretty difficult for the examiners to create a climate and tasks that are conducive to both promoting flow state performance and deliberate practice at the same time.
I’d love to hear any thoughts that others may have about this.
Heather » 27 Jan 2017 »
I have been familiar with the concept of flow as well as deliberate practice for a while but only made the connection between the two very recently.
I am curious where you came up with the determination that deliberate practice tends to be on the anxiety side of the flow channel. In my experience, a lot of the deliberate practice I’ve seen has to do with training muscle memory – so the first part of practice requires concentration/anxiety as you learn the notes or letter forms etc for the first time, and then it becomes a matter of repeating shapes or notes or hand movements over and over again for hours until your muscles begin to gain a memory of their own and less thinking is needed to perform the action.
This second phase of deliberate practice seems to me to be more on the edge of boredom than anxiety and I’ve found it a particular challenge to keep going so I usually cap practice at an hour each day for each skill I want to practice. I WANT this second phase to be more challenging, but I’m not sure how to make it so. Would love to hear your thoughts!
Malcolm » 28 Jan 2017 »
My understanding happens that learning happens more rapidly when the experience is somewhat intense. If it’s not challenging, try going faster, or more precisely, or adding more components. I’m not sure how well this generalizes between skills though. What specific skills are you attempting to become really good at?
(This Top Performer course by Scott H Young and Cal Newport is potentially a great resource for learning how to get really good at something.)
Heather » 30 Jan 2017 »
Hi Malcolm, thanks for your response! I am speaking more to the mundane muscle memory training that occurs during the deliberate practice stage for many skills:
– the “shooting 500 hoops every day” portion of training to be better at free throws,
– the “practicing the same scale over and over and over again” portion of learning an instrument
– the “memorize letter forms by repeating the letter form over and over and over again” when learning hand lettering.
The first 20 – 50 times you do this you will be challenged more than before because you’re learning a new skill, but after the practice becomes habit, I’ve found that there is a significant plummet in the challenge of an activity because your muscles are successfully learning – meaning you don’t have to concentrate as much.
For some of the above skills i can see how adding variety to your practice will keep the challenge level higher while also increasing your skill level, but hand lettering is one where I get stumped.
My first page of lowercase “a’s” may be significantly challenging, but the third time I’m going around the alphabet, that full page of “a’s” is more of a huge challenge to finish because of boredom rather than a huge challenge to finish because of difficulty level (this is when i switch to creating full compositions rather than repeating one letter over and over which solves this problem, but repeating letter forms is a MUST for mastery, and unfortunately in my experience, this is the “non-flow” portion of my day and requires me to switch to get into flow (however I’m still making progress towards my goal of mastery because I’m continuing to build towards muscle memory).
What are your thoughts?
Tom » 4 Jan 2020 »
“Essentially, you want to be performing in a flow state, but training using deliberate practice.”
Totally — and we can look at this through another lens with Stephen Covey’s concept of the P/PC Balance.
To be effective, you must strike a healthy balance between Production (in an engaging, pleasant Flow state) and Production Capability (in a stretched, unpleasant Deliberate Practice state — or in a relaxed, rejuvenating, renewing state of recuperation).
Overindex on one to the neglect of the other, and you either won’t improve past your current skill level (not enough PC of the deliberate practice kind), will burn out (not enough PC of the renewal kind), or won’t produce anything of value (not enough P).
Have your say!